Index décomplexé

27 sept 2019 - 9 minutes de lecture

Index terminologique : permet au lecteur de localiser rapidement un élément dans l’ouvrage, sans être contraint de le lire intégralement. (Wikipédia)

Index de base de données : structure de données qui permet de retrouver rapidement les données. (Wikipédia)

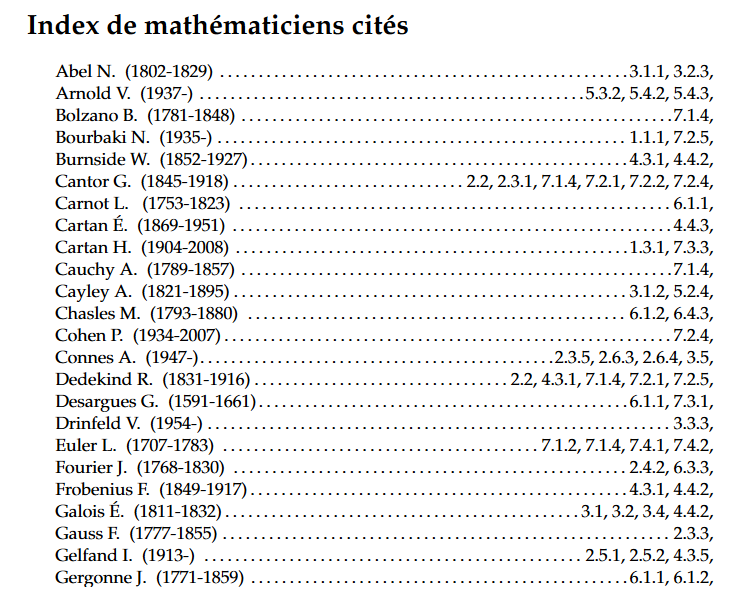
L’usage du même mot n’est pas fortuit. Chacun de ces usages désigne la capacité d’identifier rapidement un mot, un terme (ou plus largement, une donnée) à l’aide d’une adresse, comme un numéro de page, ou l’emplacement de la donnée sur un disque ou un volume. D’une façon purement scolaire, prenons le mécanisme d’indexation le plus simple : celui basé sur le tri alphanumérique. Lorsque l’on parcoure l’index pour retrouver un concept dans un livre, les propositions sont classiquement dressées dans l’ordre alphanumérique de haut en bas, de la page de gauche à la page de droite (pour de la littérature occidentale).

Ainsi, le lecteur peut démarrer sa recherche à partir de la première lettre de son mot, le comparer aux termes triés, recommencer avec la deuxième lettre, etc. jusqu’à identifier le terme voulu ou la racine la plus proche. Le résultat est alors accompagné d’une liste de numéros de pages, dans lesquelles l’auteur du livre a reférencé de lui-même les concepts-clés nécessaires à la recherche par index.

Pour ce qui est d’une base de données dite relationnelle, les informations relatives à une entité (ou objet), seront réparties dans les colonnes d’une ou de plusieurs tables. L’accès aux données est similaire à la recherche d’un mot dans un livre : critère de sélection (un nom de famille, une époque, une jointure, etc.) et un chemin d’accès (le tri alphanumérique pour faire simple).

En SQL, pour obtenir une portion de données non indexées d’une table (la liste des pages mentionnant un mathématicien, par exemple), nous demandons au moteur de parcourir la totalité des lignes et de ne retourner que la sélection voulue. Cette recherche est aussi efficace que de feuilleter un livre intégralement avant de tomber sur l’information.

La méthode d’accès pour récupérer la liste des mathématiciens ayant fait partie de la famille Gauss peut être obtenue avec l’ordre EXPLAIN suivie de la requête SELECT :

EXPLAIN (ANALYZE,BUFFERS) 
 SELECT firstname, lastname
   FROM mathematicians
  WHERE lastname = 'Gauss';

Le résultat correspond au plan d’exécution ou query plan, que le moteur construit à partir des statistiques mises à sa disposition, telles que le nombre de lignes connues dans la table, la présence d’index ou la ventilation des données selon leur valeur (aussi appelée histogramme). Durant cette première étape, le moteur peut établir plusieurs plans pour n’en conserver qu’un seul dont le coût d’exécution serait le moins élevé et garantir un temps global de traitement le plus rapide possible.

                   QUERY PLAN 
-------------------------------------------------
Seq Scan on mathematicians  
 (cost=0.00..14.33 rows=1 width=18) 
 (actual time=0.188..0.189 rows=0 loops=1)
  Filter: ((lastname)::text = 'Gauss'::text)
  Rows Removed by Filter: 666
  Buffers: shared hit=6
Planning Time: 0.229 ms
Execution Time: 0.219 ms

Le nœud Seq Scan nous confirme que la table a été lue de façon séquentielle et intégrale, bien qu’un filtre ait été appliqué. L’option ANALYZE enrichit le résultat, en contrepartie d’une véritable exécution de la requête sur les relations de la base (ici, la table mathematicians). On y retrouve dès lors le temps réel de recherche et le nombre de lignes retournées et ignorées. L’option BUFFERS indique le nombre de blocs parcourus en précisant s’ils sont lus à partir de la mémoire partagée (shared hit) ou du disque (read).

Observons à présent le comportement du moteur et le plan d’exécution qu’il propose lorsque ce dernier prend connaissance d’un index sur la colonne de recherche lastname :

                          QUERY PLAN 
--------------------------------------------------------------
Index Scan using mathematicians_lastname_idx on mathematicians  
 (cost=0.28..8.29 rows=1 width=18)
 (actual time=0.043..0.046 rows=1 loops=1)
  Index Cond: ((lastname)::text = 'Gauss'::text)
  Buffers: shared hit=3
Planning Time: 0.176 ms
Execution Time: 0.081 ms

Cette fois-ci, le moteur estime un coût de 8,29 au lieu de 14,33 à l’aide de cet index sur la condition de recherche. On constate un changement dans le nœud envisagé par le moteur : un parcours par Index Scan identifie l’unique adresse pour la valeur « Gauss » et récupère les informations connexes dans la table mathematicians. Il en résulte une réduction du nombre de blocs parcourus de 3 au lieu de 6 dans l’exemple sans index. Le gain sur le temps d’exécution est non négligeable : la requête a mis 81 µs au lieu de 219.

Cependant, cette situation n’est pas immuable et selon la valeur de la recherche, le plan d’exécution sélectionné peut varier. Prenons l’exemple des mathématiciens de la famille Cartan.

                          QUERY PLAN 
--------------------------------------------------------------
Bitmap Heap Scan on mathematicians
 (cost=4.29..8.85 rows=2 width=18) 
 (actual time=0.067..0.072 rows=2 loops=1)
  Recheck Cond: ((lastname)::text = 'Cartan'::text)
  Heap Blocks: exact=2
  Buffers: shared hit=4
  ->  Bitmap Index Scan on mathematicians_lastname_idx
       (cost=0.00..4.29 rows=2 width=0) 
       (actual time=0.051..0.051 rows=2 loops=1)
        Index Cond: ((lastname)::text = 'Cartan'::text)
        Buffers: shared read=2
Planning Time: 0.173 ms
Execution Time: 0.119 ms

Nous avons affaire à un autre nœud relatif à l’usage d’un index, le Bitmap Heap Scan et son Bitmap Index Scan. Le moteur a trouvé dans son parcours d’index, deux lignes (rows=2) dont il stocke les adresses dans un tableau en mémoire, aussi appelé bitmap. La récupération des lignes provoque des accès dits aléatoires et peut devenir coûteuse pour le moteur.

Pour les opérations de comparaison simple comme l’égalité, il est recommandé d’utiliser un index b-tree, par défaut avec l’ordre CREATE INDEX. Cet index s’appuie sur un algorithme du même nom qui assure le stockage des couples valeur/adresse au sein d’un arbre dit équilibré, dont la profondeur doit être la plus faible possible pour réduire les coûts de lecture.

Un index b-tree est composé :

• d’un bloc méta ;
• de blocs intermédiaires, dont le bloc racine (root) ;
• de blocs feuilles.

Il est possible de les consulter à l’aide des fonctions mises à disposition par les extensions pgstattuple et pageinspect, et de démêler le parcours d’index que réalise le moteur à chaque exécution.

 SELECT bt_page_stats.blkno, type, live_items
   FROM generate_series(1,
          pg_relpages('mathematicians_lastname_idx')::integer-1
        ) blkno,
LATERAL bt_page_stats('mathematicians_lastname_idx', blkno);

--  blkno | type | live_items 
-- -------+------+------------
--      1 | l    |        317
--      2 | l    |        319
--      3 | r    |          3
--      4 | l    |         32

Requête issue de « PostgreSQL Architecture et notions avancées » de Guillaume Lelarge, édition D-BookeR.

La méthode bt_page_stats associée au nom de l’index et le numéro du bloc, peut être couplée avec la fonction generate_series pour obtenir une ligne par bloc appartenant à l’index, à l’exception du bloc méta. On constate que le bloc n°3 est la racine (type=r) de notre b-tree, bloc à partir duquel le moteur pourra réaliser les comparaisons successives jusqu’à atteindre les valeurs de sa recherche.

SELECT ctid, data, convert_from(decode(
         substring(replace(data, ' 00', ''), 4), 
       'hex'), 'utf8') as text
  FROM bt_page_items('mathematicians_lastname_idx', 3);

--   ctid   |                      data                       |     text     
-- ---------+-------------------------------------------------+--------------
--  (1,0)   |                                                 | 
--  (2,38)  | 0f 4b 6c 65 65 6e 65 00                         | Kleene
--  (4,116) | 1b 5a 61 72 61 6e 6b 69 65 77 69 63 7a 00 00 00 | Zarankiewicz

Le bloc racine nous indique qu’il existe trois ramifications (comme l’indiquaient les statistiques précédentes avec la valeur live_items du bloc n°3) contenant les adresses physiques aussi appellées ctid. Le champs data varie selon le type de donnée indexée et s’il s’agit d’un bloc d’index ou d’un bloc de table ; dans cet exemple, la colonne text nous indique la borne basse (minus infinity) de chaque bloc. Il est possible d’obtenir les extrêmes de chaque bloc feuille avec la requête suivante :

SELECT blkno, min(text), max(text)
  FROM (
    SELECT blkno, convert_from(decode(
            substring(replace(data, ' 00', ''), 4), 
            'hex'), 'utf8') as text
      FROM (
        SELECT bt_page_stats.blkno 
          FROM generate_series(1,
                 pg_relpages('mathematicians_lastname_idx')::integer-1
               ) blkno,
        LATERAL bt_page_stats('mathematicians_lastname_idx', blkno)
          WHERE type = 'l'
      ) blkno,
   LATERAL bt_page_items('mathematicians_lastname_idx', blkno)
     WHERE length(data) > 0
  ) t GROUP BY blkno ORDER BY blkno;

--  blkno |     min      |     max      
-- -------+--------------+--------------
--      1 | Abbt         | Kleene
--      2 | Kleene       | Zarankiewicz
--      4 | Zarankiewicz | Zygmund

Pour nos exemples de recherche, les noms « Gauss » et « Cartan » sont tous deux classés entre les lettres A et K, soit dans le bloc n°1 de l’index mathematicians_lastname_idx. Le parcours se poursuit donc dans ce nouveau bloc feuille, où les adresses ctid correspondent à présent aux blocs physiques de la table mathematicians.

SELECT *
  FROM (
    SELECT ctid, data, convert_from(decode(
             substring(replace(data, ' 00', ''), 4), 
           'hex'), 'utf8') as text
      FROM bt_page_items('mathematicians_lastname_idx', 1)
  ) t
 WHERE text IN ('Gauss', 'Cartan');

--   ctid   |          data           |  text  
-- ---------+-------------------------+--------
--  (3,8)   | 0f 43 61 72 74 61 6e 00 | Cartan
--  (4,8)   | 0f 43 61 72 74 61 6e 00 | Cartan
--  (1,102) | 0d 47 61 75 73 73 00 00 | Gauss

Les résultats des plans d’exécution précédents s’expliquent ! Pour rappel, nous avions un nœud Index Scan pour la recherche « Gauss » et deux nœuds Bitmap Heap/Index Scan pour la recherche Cartan.

La première recherche effectue physiquement deux lectures dans l’index (blocs 3 puis 1) avant de lire le bloc de données (1,102), soit un total de trois blocs, cohérent avec le plan d’exécution (Buffers: shared hit=3).

La seconde recherche effectue également deux lectures dans l’index mais ira récupérer deux lignes distinctes à deux endroits différents de la table (adresses (3,8) et (4,8)), soit un total de quatre blocs, valeur également annoncée par le plan (Buffers: shared hit=4).

Bien évidemment, la consultation du contenu des index n’est pas nécessaire pour l’analyse de performances. Ces derniers vivent et s’équilibrent à chaque modification de données pour maintenir les adresses physiques et garantir un accès optimisé avec la profondeur de lecture la plus faible possible.

L’ajout d’un index ne doit pas être un réflexe systèmatique. Il faut tenir compte de la cardinalité des données d’une colonne, autrement dit, la faible proportion de données retournée à chaque filtre. Dans le cas de la table mathematicians, une recherche basée sur les conditions LIKE ou > pourrait très simplement parcourir l’ensemble des six blocs de la table (Seq Scan), car moins coûteux que le parcours de plusieurs blocs d’index supplémentaires.

Cet article s’est concentré sur le fonctionnement de l’index le plus courant b-tree mais il en existe encore d’autres, répondant à des contraintes variées de recherche et de stockage !